cs
Steap 与 Queap
-
04.Stack + Queue.pdf P93
-
习题解析[10-19]、[10-20]
Stack / Queue + Heap,让栈和队列能getMax()
思路为:一个普通的栈/队列,加上记录前缀max
Steap
栈 + getMax
左为栈底,右为栈顶:[...>,原栈为S,用P记录前缀max,这里P只需要是个stack就行了。
pop/push时,对S进行操作,同时,由于增加/减少元素都在右侧尾部,所以对P中间的位置 $i$,其前缀是没有变化的,对P的维护只需 $O(1)$ 时间,以push一个元素为例,只需:P[last] = max(P[last - 1], S[last]) 即可完成P的维护。
优化:将 P 中的相邻相等元素压缩记 $cnt$。能优化空间,时间复杂度不变。
push/pop $O(1)$ ,getMax $O(1)$
Queap
队列 + getMax
左为队尾,右为队首,同样P记录前缀max,这个P要访问中间,得是个vector/list。
若Q元素出队,则P也只需出队;
但是若Q元素入队,则P的所有元素的前缀都变了,所有位置的前缀max都要重新算。遍历过程当发现某个位置的前缀max没变,循环可以提前退出,但是最坏情况下enqueue仍需要 $O(n)$ 时间,且若按单调增加的顺序enqueue元素,最坏情况会持续发生。
造成这种差别的原因在于,enqueue之后,所有位置的前缀都发生了变化。
优化:同理,将 P 中的相邻相等元素压缩记 $cnt$。能优化空间,且enqueue的均摊时间复杂度能降到 $O(1)$ 。证明:
考虑 $n$ 次 enqueue 操作,单次 enqueue 的开销可能很高,但是,P 中被迭代的元素必然随即被删除并压缩入某个前驱。$n$ 次 enqueue 最多产生 $n$ 个元素,所以迭代的元素总个数只有 $O(n)$ 个,分摊下来每次enqueue只有 $O(1)$ 。
dequeue $O(1)$ ,enqueue 最坏 $O(n)$,分摊$O(1)$ ,getMax $O(1)$
双栈当队 与 双队当栈
这个东西和双队当栈都没什么用,不如直接实现,只是硬给了约束要求去实现。
主要看均摊分析的分析方法,其中一种是势能分析法。
双栈当队
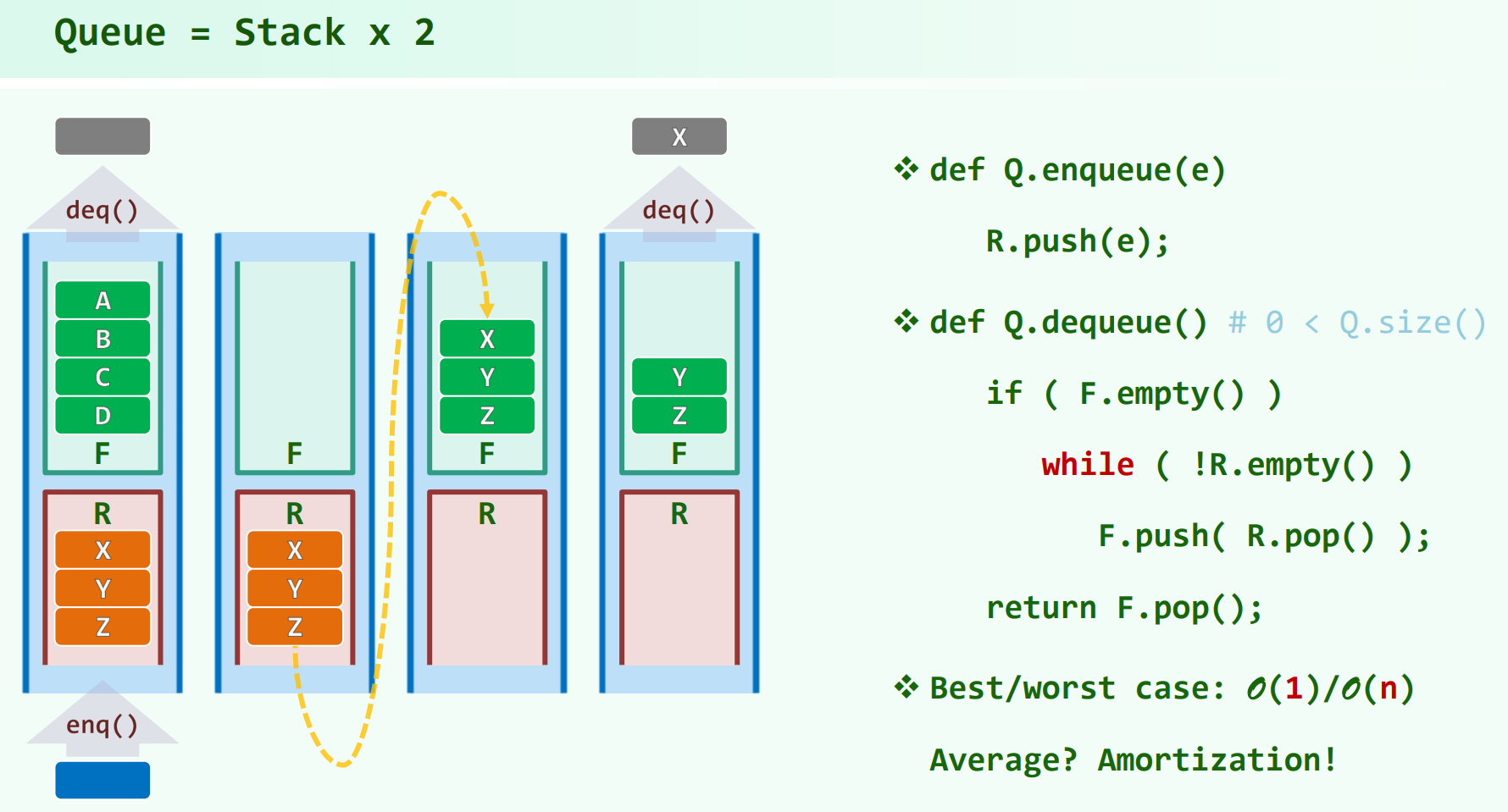
enqueue的时间复杂度为 $O(1)$
最坏情况下dequeue会是 $O(n)$ ,但是分摊时间复杂度为 $O(1)$ ,证明:
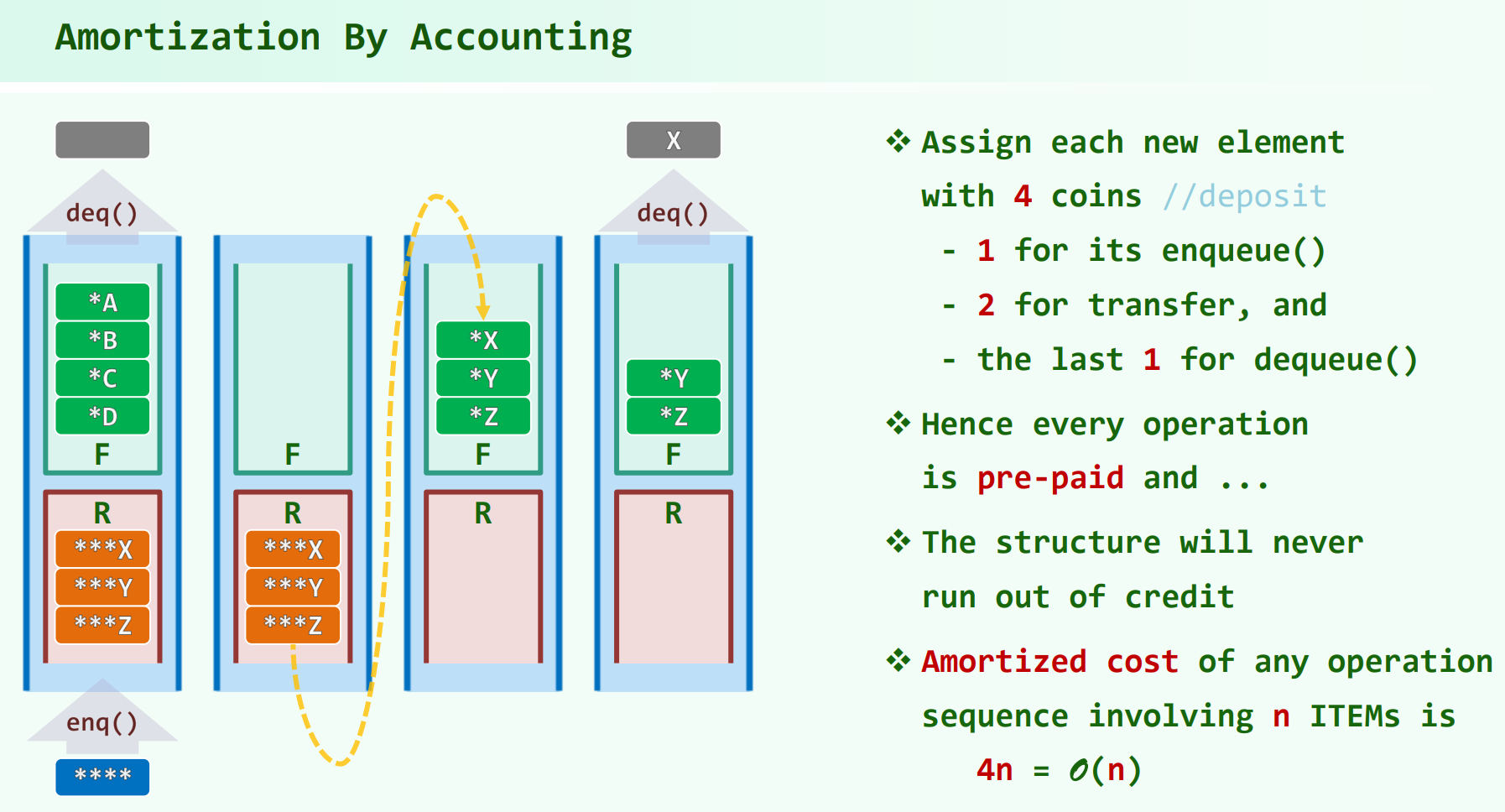
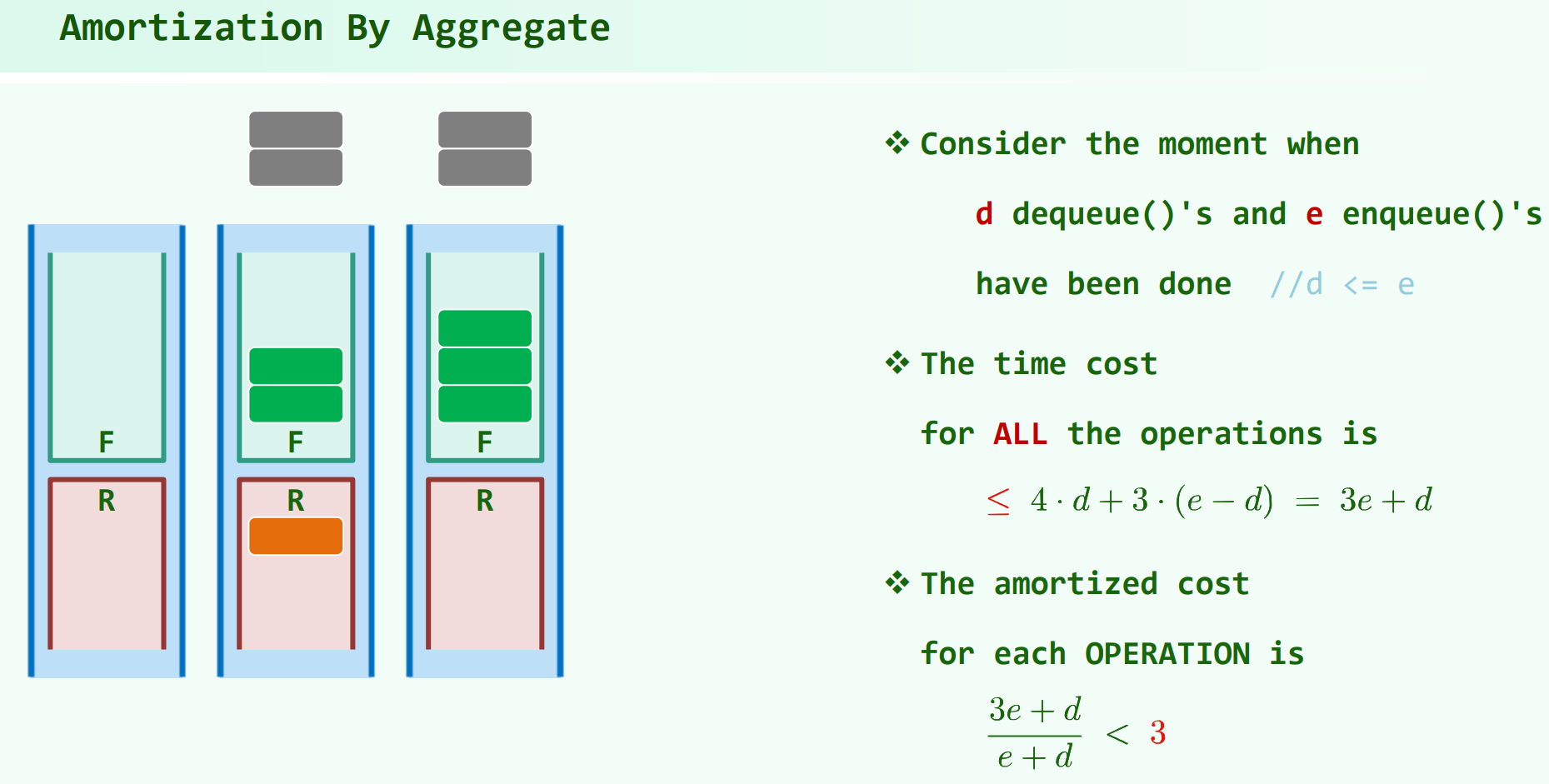
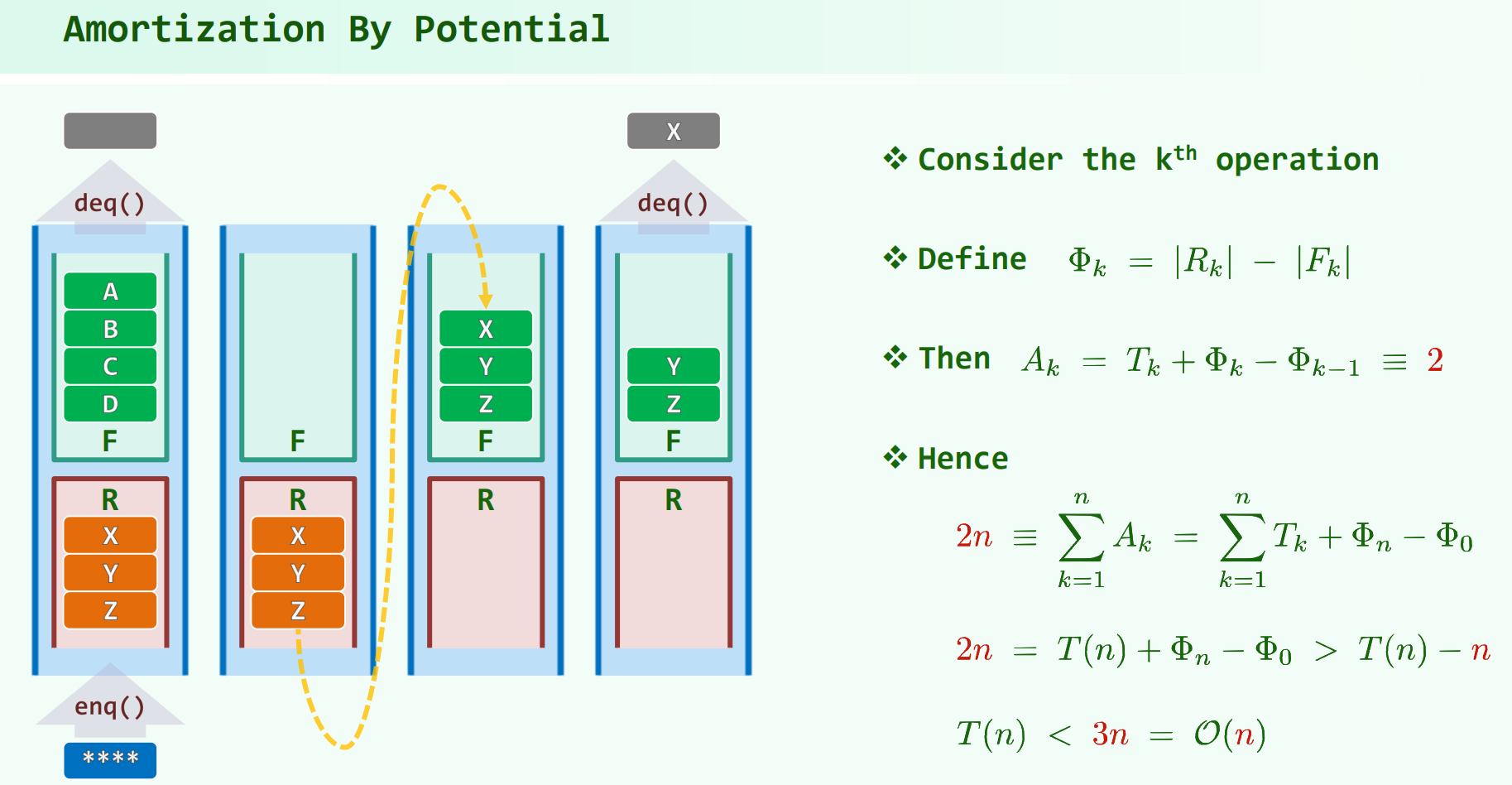
解释一下方法3这个势能分析法:
定义势能函数 $\Phi_{k} = \lvert R_k \rvert - \lvert F_k \rvert$,为栈大小的差值。
于是,均摊成本 $A_k = T_k + \Phi_{k} - \Phi_{k - 1}$ , $T_k$ 为第 $k$ 次操作的实际代价。
注意这里的分析技巧,某步的 $T_k$ 可能很大,不好分析,但是 $T_k$ 加上了 $\Phi_{k} - \Phi_{k - 1}$,某步的 $T_k$ 大,势能函数的定义就会使得 $\Phi_{k} - \Phi_{k - 1}$ 负得多。于是 $A_k \equiv 2$,是常数。这样,就把时大时小的 $T_k$ 给平均成了 $O(1)$ 的 $A_k$ 。($T_k$ 时大时小,不知道平均值,算不了总代价,但是通过构造能知道 $A_k$ 是 $O(1)$)
于是,$\sum A_k = \sum T_k + \Phi_{k} - \Phi_{0}$,而 $\sum A_k = 2n,\Phi_{k} = O(n)$,故 $\sum T_k = O(n)$。
$n$ 次操作的总时间复杂度 $\sum T_k = O(n)$ ,于是分摊到每次为 $O(1)$
双队当栈
双队当栈,会发现把两个栈首尾相接怎么都仍是先进先出,所以不能用双栈当队的思路。
一个元素x入队后,要让其先出,必须将其前面的元素都弄到x的后面去,所以需要把前面的元素出队后重新入队。这个过程可以借助第二个队列,不过实际单用一个队列就可以完成了,第二个队列实际是不必要的。
push的时间复杂度 $O(n)$ ,均摊也是 $O(n)$ 级别的
pop的时间复杂度 $O(1)$